题目链接：

题意：给定一个图。判断是不是弦图？

思路：（1）神马是弦图？对于一个无向图，若该图的任意一个长度大于3的环中存在一条边连接这个环上不相邻的两点，则此图称作弦图。

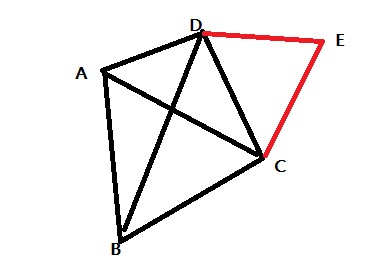
（2）什么是团？团是原图的一个子图，子图就是包含了原图的某些点，那么就要包含这些点之间的边。并且团不是一般的子图而是一个完全子图，就是这个子图的任意两个顶点之间都有边。下面的ABCD就是原图的一个团。

（3）完美消除序列：原图的一个点的序列(每个点出现且恰好出现一次)v1, v2,……, vn满足{vi, vi+1,…,vn}的组成的子图为团。

（4）一个无向图是弦图当且仅当它有一个完美消除序列。

（5）如何计算完美消除序列？最大势算法： 从n到1的顺序依次给点标号(标号为i的点出现在完美消除序列的第i个)。 设label[i]表示第i个点与多少个已标号的点相 邻，每次选择label[i]最大的未标号的点进行标号。注意这里只是计算出了完美消除序列，但是在求出这个之后还没有判定是不是弦图。

（6）如何从完美消除序列判断原图是不是弦 图？最朴素的办法是依次判断 {vi+1,…,vn}中所有与vi相邻的点是否构成了一个团。可以这样优化：设{vi+1,…,vn}中所有与vi相邻的点依次为 vj1,……,vjk。只需判断vj1是否与vj2,……,vjk相邻即可。

 

int n,m,g[N][N];int d[N],a[N],h[N],p[N];int OK(){    int i,j,u;    vector
     
       V;    FORL1(i,n)    {        V.clear();        FOR1(j,n) if(g[a[i]][j]) if(p[j]>i) V.pb(j);        for(j=1;j
      
       p[V[j]])        {            swap(V[0],V[j]);        }        for(j=1;j
       
        u) u=d[j],k=j;            a[i]=k; h[k]=1; p[k]=i;            FOR1(j,n) if(g[k][j]) d[j]++;        }        if(OK()) puts("Perfect");        else puts("Imperfect");        puts("");    }    return 0;}